Portal:Mathematics

The Mathematics Portal

Carl Friedrich Gauss

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.

---

• 

  

  
  Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
  
  Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
• 

  

  Plots of logarithm functions, with three commonly used bases. The special points log_b b = 1 are indicated by dotted lines, and all curves intersect in log_b 1 = 0.

  
  
  In mathematics, the logarithm to base b is the inverse function of exponentiation with base b. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 10³, the logarithm base $10$ of 1000 is 3, or log₁₀ (1000) = 3. The logarithm of x to base b is denoted as log_b (x), or without parentheses, log_b x. When the base is clear from the context or is irrelevant it is sometimes written log x.
  
  The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number e ≈ 2.718 as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base 2 and is frequently used in computer science. (Full article...)
• 
  General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.
  
  Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
• 

  

  
  Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.
  
  In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
• 
  
  

  

  Archimedes Thoughtful
  by Domenico Fetti (1620)

  
  Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is considered one of the leading scientists in classical antiquity. Regarded as the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.
  
  Archimedes' other mathematical achievements include deriving an approximation of pi (π), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
• 

  

  The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

  
  
  In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
  $$\sum _{n=1}^{m}n(-1)^{n-1}.$$
  
  The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
  $$1-2+3-4+\cdots ={\frac {1}{4}}.$$ (Full article...)
• 
  
  

  

  A stamp of Zhang Heng issued by China Post in 1955

  
  Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.
  
  Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
• 

  

  The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

  
  The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
  
  A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 
  
  

  

  One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

  
  Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.
  
  Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
• 

  

  Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

  
  
  In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
  
  In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
• 

  

  Logic studies valid forms of inference like modus ponens.

  
  
  Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
  
  Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
• 
  In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
  
  Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
• 
  In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
  
  The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)

Selected image –

a smooth surface, vaguely conical in shape and embedded in a basket-like mesh of points, rotates in empty space

Non-uniform rational B-spline

Credit: Greg L

Non-uniform rational B-splines (NURBS) are commonly used in computer graphics for generating and representing curves and surfaces for both analytic shapes (described by mathematical formulas) and modeled shapes. Here the shape of the surface is determined by control points, shown as small spheres surrounding the surface itself. The square at the bottom sets the maximum width and length of the surface. Based on early work by Pierre Bézier and Paul de Casteljau, NURBS are generalizations of both B-splines (basis splines) and Bézier curves and surfaces. Unlike simple Bézier curves and surfaces, which are non-rational, NURBS can represent exactly certain analytic shapes such as conic sections and spherical sections. They are widely used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE), although T-splines and subdivision surfaces may be more suitable for more complex organic shapes.

Good articles –

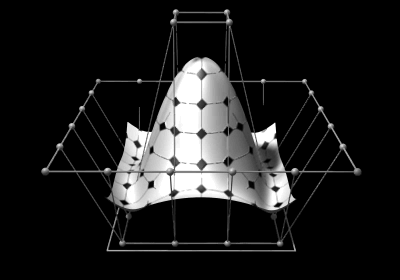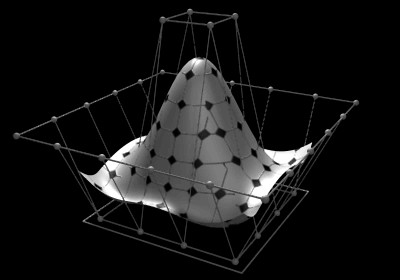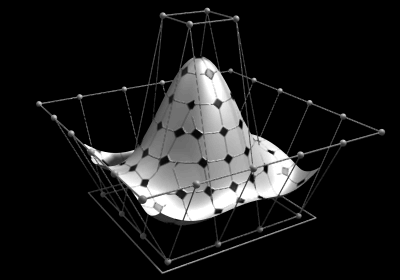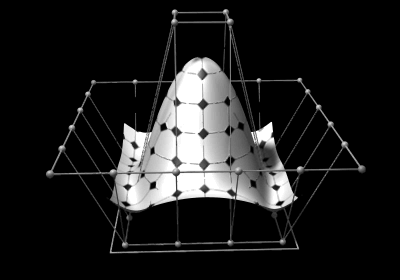
  These are Good articles, which meet a core set of high editorial standards.

---

• 

  

  Graphical demonstration of the convergence of the sum 1/2 + 1/3 + 1/7 + 1/43 + ... to 1. Each row of k squares of side length 1/k has total area 1/k, and all the squares together exactly cover a larger square with area 1. Squares with side lengths 1/1807 or smaller are too small to see in the figure and are not shown.

  
  In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. Its first few terms are
  :2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443 (sequence A000058 in the OEIS).
  
  Sylvester's sequence is named after James Joseph Sylvester, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series of unit fractions that converges to 1 more rapidly than any other series of unit fractions. The recurrence by which it is defined allows the numbers in the sequence to be factored more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its terms. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian Einstein manifolds, and hard instances for online algorithms. (Full article...)
• 

  

  A Doyle spiral of type (8,16) printed in 1911 in Popular Science as an illustration of phyllotaxis. One of its spiral arms is shaded.

  
  In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes.
  
  Doyle spirals are named after mathematician Peter G. Doyle, who made an important contribution to their mathematical construction in the late 1980s or early 1990s. However, their study in phyllotaxis (the mathematics of plant growth) dates back to the early 1900s. (Full article...)
• 

  

  Title page of De quinque corporibus regularibus

  
  De quinque corporibus regularibus (sometimes called Libellus de quinque corporibus regularibus) is a book on the geometry of polyhedra written in the 1480s or early 1490s by Italian painter and mathematician Piero della Francesca. It is a manuscript, in the Latin language; its title means [the little book] on the five regular solids. It is one of three books known to have been written by della Francesca.
  
  Along with the Platonic solids, De quinque corporibus regularibus includes descriptions of five of the thirteen Archimedean solids, and of several other irregular polyhedra coming from architectural applications. It was the first of what would become many books connecting mathematics to art through the construction and perspective drawing of polyhedra, including Luca Pacioli's 1509 Divina proportione (which incorporated without credit an Italian translation of della Francesca's work). (Full article...)
• 
  In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation.
  
  There are multiple different notations for differentiation, two of the most commonly used being Leibniz notation and prime notation. Leibniz notation, named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas prime notation is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leibniz notation by adding superscripts to the differentials, and in prime notation by adding additional prime marks. The higher order derivatives can be applied in physics; for example, while the first derivative of the position of a moving object with respect to time is the object's velocity, how the position changes as time advances, the second derivative is the object's acceleration, how the velocity changes as time advances. (Full article...)
• 
  In mathematics, the three-gap theorem, three-distance theorem, or Steinhaus conjecture states that if one places n points on a circle, at angles of θ, 2θ, 3θ, ... from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. When there are three distances, the largest of the three always equals the sum of the other two. Unless θ is a rational multiple of π, there will also be at least two distinct distances.
  
  This result was conjectured by Hugo Steinhaus, and proved in the 1950s by Vera T. Sós, János Surányi, and Stanisław Świerczkowski; more proofs were added by others later. Applications of the three-gap theorem include the study of plant growth and musical tuning systems, and the theory of light reflection within a mirrored square. (Full article...)
• 

  

  A well-covered graph, the intersection graph of the nine diagonals of a hexagon. The three red vertices form one of its 14 equal-sized maximal independent sets, and the six blue vertices form the complementary minimal vertex cover.

  
  In graph theory, a well-covered graph is an undirected graph in which the minimal vertex covers all have the same size. Here, a vertex cover is a set of vertices that touches all edges, and it is minimal if removing any vertex from it would leave some edge uncovered. Equivalently, well-covered graphs are the graphs in which all maximal independent sets have equal size. Well-covered graphs were defined and first studied by Michael D. Plummer in 1970.
  
  The well-covered graphs include all complete graphs, balanced complete bipartite graphs, and the rook's graphs whose vertices represent squares of a chessboard and edges represent moves of a chess rook. Known characterizations of the well-covered cubic graphs, well-covered claw-free graphs, and well-covered graphs of high girth allow these graphs to be recognized in polynomial time, but testing whether other kinds of graph are well-covered is a coNP-complete problem. (Full article...)
• 
  Paterson's worms are a family of cellular automata devised in 1971 by Mike Paterson and John Horton Conway to model the behaviour and feeding patterns of certain prehistoric worms. In the model, a worm moves between points on a triangular grid along line segments, representing food. Its turnings are determined by the configuration of eaten and uneaten line segments adjacent to the point at which the worm currently is. Despite being governed by simple rules the behaviour of the worms can be extremely complex, and the ultimate fate of one variant is still unknown.
  
  The worms were studied in the early 1970s by Paterson, Conway and Michael Beeler, described by Beeler in June 1973, and presented in November 1973 in Martin Gardner's "Mathematical Games" column in Scientific American. (Full article...)
• 
  In mathematics and computer science, the BIT predicate, sometimes written ${\text{BIT}}(i,j)$, is a predicate that tests whether the $j$th bit of the number $i$ (starting from the least significant digit) is 1, when $i$ is written as a binary number. Its mathematical applications include modeling the membership relation of hereditarily finite sets, and defining the adjacency relation of the Rado graph. In computer science, it is used for efficient representations of set data structures using bit vectors, in defining the private information retrieval problem from communication complexity, and in descriptive complexity theory to formulate logical descriptions of complexity classes. (Full article...)
• 

  

  The regular heptagon cannot be constructed using only a straightedge and compass construction; this can be proven using the field of constructible numbers.

  
  In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.
  
  The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as fields of rational functions, algebraic function fields, algebraic number fields, and p-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Most cryptographic protocols rely on finite fields, i.e., fields with finitely many elements. (Full article...)
• 
  In control system theory, and various branches of engineering, a transfer function matrix, or just transfer matrix is a generalisation of the transfer functions of single-input single-output (SISO) systems to multiple-input and multiple-output (MIMO) systems. The matrix relates the outputs of the system to its inputs. It is a particularly useful construction for linear time-invariant (LTI) systems because it can be expressed in terms of the s-plane.
  
  In some systems, especially ones consisting entirely of passive components, it can be ambiguous which variables are inputs and which are outputs. In electrical engineering, a common scheme is to gather all the voltage variables on one side and all the current variables on the other regardless of which are inputs or outputs. This results in all the elements of the transfer matrix being in units of impedance. The concept of impedance (and hence impedance matrices) has been borrowed into other energy domains by analogy, especially mechanics and acoustics. (Full article...)
• 
  The Math Myth: And Other STEM Delusions is a 2016 nonfiction book by Queens College political scientist Andrew Hacker analyzing and critiquing the United States educational system's teaching of mathematics as a linear progression towards more advanced fields. Based on a 2012 New York Times op-ed by Hacker titled "Is Algebra Necessary", Hacker argues that the teaching of advanced algebra, trigonometry, and calculus is not useful to the majority of students. He further claims that the requirement of advanced mathematics courses in secondary education contributes to dropout rates and impedes socioeconomically disadvantaged students from pursuing further education. Hacker critiques the Common Core system and American focus on STEM education in lieu of social sciences, arguing that the educational system should prioritize numeracy over pure mathematics education.
  
  The Math Myth received broadly critical coverage from critics and mathematicians, some citing Hacker's arguments as "disingenuous" and contributing to an elitist attitude towards mathematics, with many citing a lack of exploration on mathematics in early childhood and primary education. Others praised Hacker's work, describing the book as offering a convincing critique of STEM education in the United States and empowering to students struggling in mathematics. (Full article...)
• 
  Stanisław Marcin Ulam (Polish: [sta'ɲiswaf 'mart͡ɕin 'ulam]; 13 April 1909 – 13 May 1984) was a Polish mathematician, nuclear physicist and computer scientist. He participated in the Manhattan Project, originated the Teller–Ulam design of thermonuclear weapons, discovered the concept of the cellular automaton, invented the Monte Carlo method of computation, and suggested nuclear pulse propulsion. In pure and applied mathematics, he proved a number of theorems and proposed several conjectures.
  
  Born into a wealthy Polish Jewish family in Lemberg, Austria-Hungary; Ulam studied mathematics at the Lwów Polytechnic Institute, where he earned his PhD in 1933 under the supervision of Kazimierz Kuratowski and Włodzimierz Stożek. In 1935, John von Neumann, whom Ulam had met in Warsaw, invited him to come to the Institute for Advanced Study in Princeton, New Jersey, for a few months. From 1936 to 1939, he spent summers in Poland and academic years at Harvard University in Cambridge, Massachusetts, where he worked to establish important results regarding ergodic theory. On 20 August 1939, he sailed for the United States for the last time with his 17-year-old brother Adam Ulam. He became an assistant professor at the University of Wisconsin–Madison in 1940, and a United States citizen in 1941. (Full article...)

Did you know (auto-generated) –

• ... that two members of the French parliament were killed when a delayed-action German bomb exploded in the town hall at Bapaume on 25 March 1917?
• ... that in 1967 two mathematicians published PhD dissertations independently disproving the same thirteen-year-old conjecture?
• ... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
• ... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
• ... that more than 60 scientific papers authored by mathematician Paul Erdős were published posthumously?
• ... that people in Madagascar perform algebra on tree seeds in order to tell the future?
• ... that Ewa Ligocka cooked another mathematician's goose?
• ... that the music of math rock band Jyocho has been alternatively described as akin to "madness" or "contemplative and melancholy"?

More did you know –

Did you know...

• ...that it is unknown whether π and e are algebraically independent?
• ...that a nonconvex polygon with three convex vertices is called a pseudotriangle?
• ...that it is possible for a three-dimensional figure to have a finite volume but infinite surface area, such as Gabriel's Horn?
• ... that as the dimension of a hypersphere tends to infinity, its "volume" (content) tends to 0?
• ...that the primality of a number can be determined using only a single division using Wilson's Theorem?
• ...that the line separating the numerator and denominator of a fraction is called a solidus if written as a diagonal line or a vinculum if written as a horizontal line?
• ...that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type the complete works of William Shakespeare?

Selected article –

A Hilbert space is a real or complex vector space with a positive-definite Hermitian form, that is complete under its norm. Thus it is an inner product space, which means that it has notions of distance and of angle (especially the notion of orthogonality or perpendicularity). The completeness requirement ensures that for infinite dimensional Hilbert spaces the limits exist when expected, which facilitates various definitions from calculus. A typical example of a Hilbert space is the space of square summable sequences.

Hilbert spaces allow simple geometric concepts, like projection and change of basis to be applied to infinite dimensional spaces, such as function spaces. They provide a context with which to formalize and generalize the concepts of the Fourier series in terms of arbitrary orthogonal polynomials and of the Fourier transform, which are central concepts from functional analysis. Hilbert spaces are of crucial importance in the mathematical formulation of quantum mechanics. (Full article...)

View all selected articles

Subcategories

Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming

---

Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Mathematics-related lists

Mathematicians

Women in mathematics

Works about mathematics

Mathematics and art

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

FL-Class Polyhedra articles

History of mathematics

Mathematics occupations

Mathematical notation

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Related portals

WikiProjects

The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

Project pages

• Participants
• Current activity
• Manual of style
• Conventions

Essays

• Advice on using Wikipedia for mathematics self-study
• Proofs

Subprojects

• PlanetMath Exchange (Talk)
• Graphics (Talk)
• Article assessment (Talk)

Related projects

Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics

Things you can do

• Create a new article: List of requested articles
• Add a new image: Image requests
• Expand an article: Mathematics stubs
• Lend your expertise: Expert attention needed

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

• 

  Commons
  Free media repository

• 

  Wikibooks
  Free textbooks and manuals

• 

  Wikidata
  Free knowledge base

• 

  Wikinews
  Free-content news

• 

  Wikiquote
  Collection of quotations

• 

  Wikisource
  Free-content library

• 

  Wikiversity
  Free learning tools

• 

  Wiktionary
  Dictionary and thesaurus

More portals

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals